Xét bài toán dao động sợi dây hai đầu cố định
$$u_{tt}-u_{xx}=0 \text{ trong } (0, L)\times(0, \infty), L=1 \text{ là chiều dài sợi dây},$$
$$u(0, t)=u(1, t)=0 \text{ khi } t\ge 0,$$
$$u(x, 0)=\begin{cases} 4x & \text{ khi } 0<x<1/4,\\ 4(1/2-x) & \text{ khi } 1/4<x<3/4,\\ 4(x-1) & \text{ khi } 3/4<x<1,\end{cases} \text{ và } u_t(x, 0)=0.$$
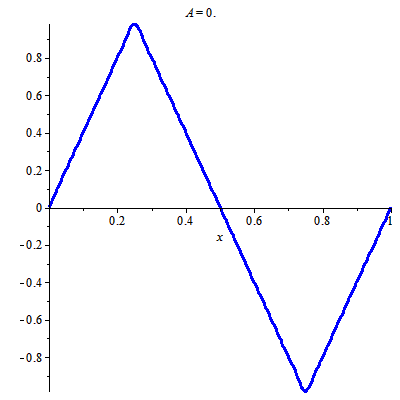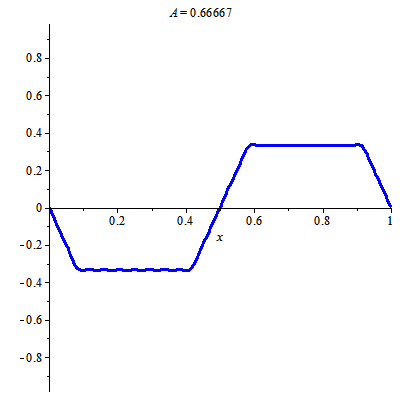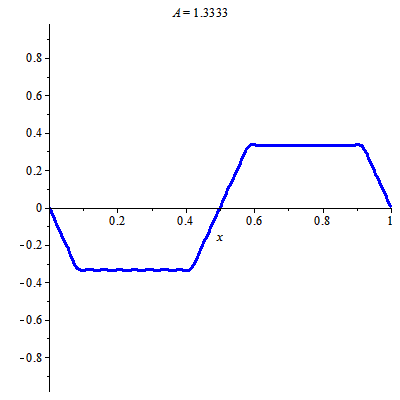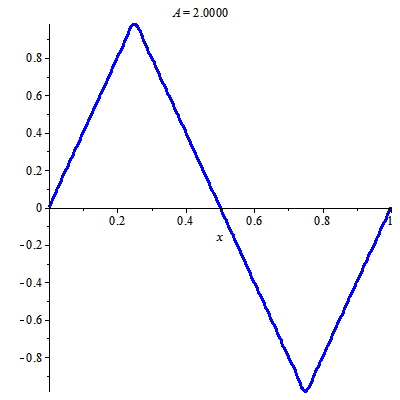
Để vẽ được hình động trên, ta cần chọn tổng riêng phù hợp của chuỗi nghiệm
$$u(x, t)=\sum\limits_{k=0}^\infty \dfrac{8(-1)^k}{\pi^2 (2k+1)^2}\cos((4k+2)\pi t)\sin((4k+2)\pi x).$$
Điều này làm được nhờ: tính phụ thuộc liên tục vào điều kiện ban đầu trong khoảng thời gian hữu hạn (tính ổn định trong khoảng thời gian hữu hạn). Ta chọn tổng riêng tại thời điểm ban đầu "đủ giống" điều kiện ban đầu. Trong trường hợp này tôi chọn $11$ số hạng đầu.
Lệnh trong Maple
> g := proc (x, t) options operator, arrow; sum(8*(-1)^k*cos((4*k+2)*Pi*t)*sin((4*k+2)*Pi*x)/(Pi^2*(2*k+1)^2), k = 0 .. 10) end proc;
> plots[animate](plot, [g(x, A), x = 0 .. 1, color = blue], A = 0 .. 2, thickness = 3);
Ví dụ khác về dao động sợi dây chiều dài $L=\pi$, với hai đầu cố định:
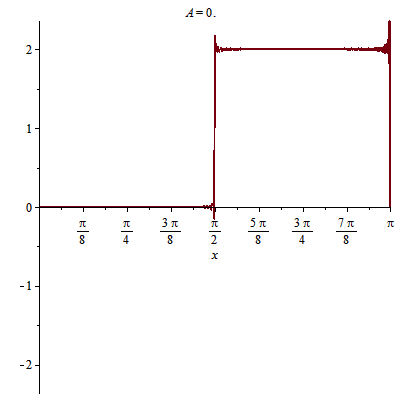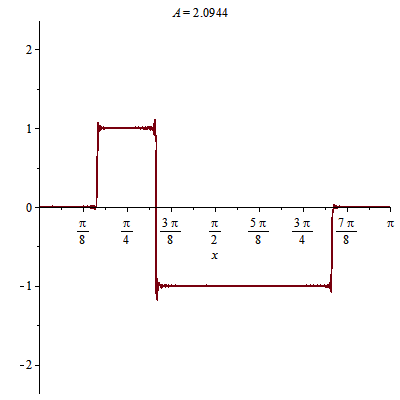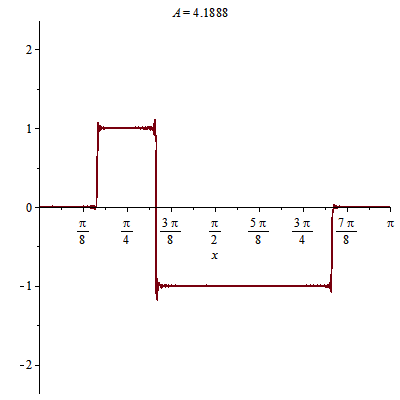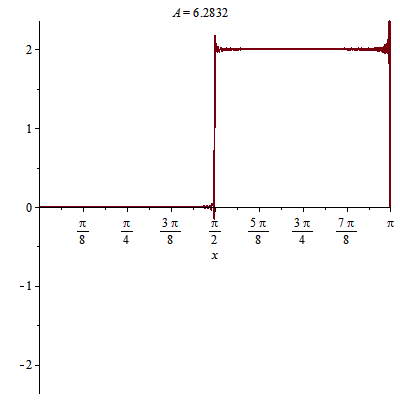
Các bạn đoán xem: điều kiện ban đầu của dao động trên?
Ví dụ về dao động của màng rung hình vuông với biên cố định
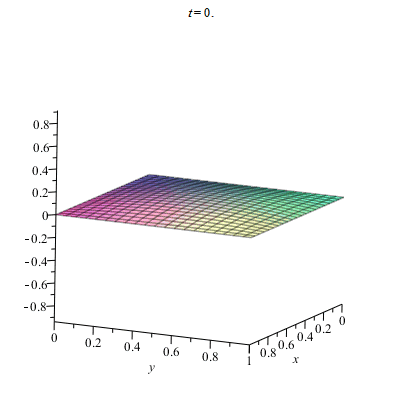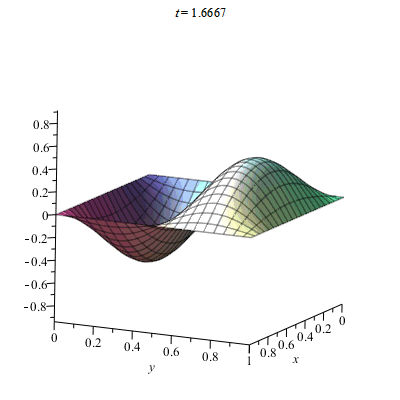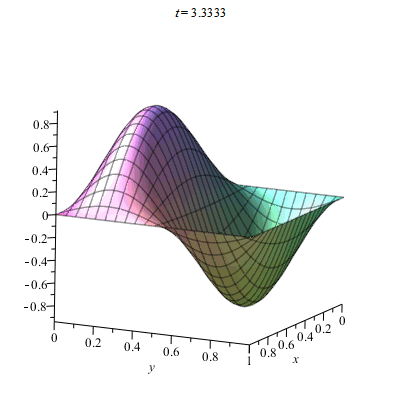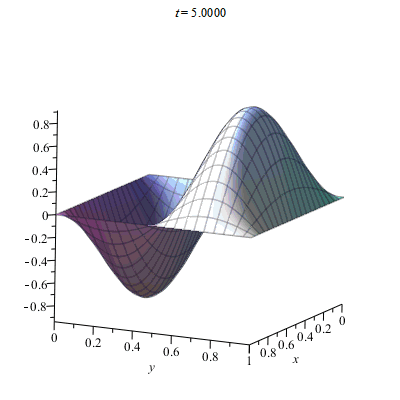
Lệnh trong Maple
> f := proc (x, y, t) options operator, arrow; sum(sum((16-16*(-1)^n)*(1-(-1)^m)*cos(t*sqrt(m^2+n^2))*sin(n*Pi*x)*sin(m*Pi*y)/(Pi^6*n^3*m^3), m = 1 .. 10), n = 1 .. 10) end proc; g(x, y) = x*(1-x)*y*(1-y); h := proc (x, y, t) options operator, arrow; 2*sin(Pi*x)*sin(2*Pi*y)*sin(t*sqrt(5))/sqrt(5) end proc
> plots[animate](plot3d, [[f(x, y, t)+h(x, y, t)], x = 0 .. 1, y = 0 .. 1, grid = [100, 100]], t = 0 .. 5)


