Trong bài này tôi sẽ trình bày việc tính toán hệ số Fourier của hàm cụ thể sau:
Hàm $J:\mathbb R\to\mathbb R$ là hàm lẻ, tuần hoàn chu kỳ $2\pi$, được xác định bởi:
$$J(x)=\frac{\pi-x}{2\pi}, 0<x\le 2\pi.$$
Hàm này có đồ thị
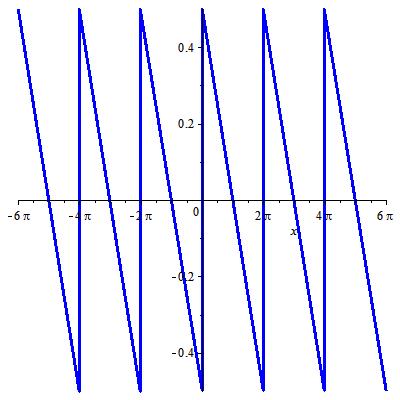
Để tính hệ số Fourier của hàm này trước hết ta nhập chu kỳ và hàm trong một chu kỳ:
> L:=2*Pi: # nhap chu ky
> J(x):=(Pi-x)/(2*Pi): # nhap ham trong chu ky (0, L)
Đồ thị trên được vẽ như sau:
> J1(x):=J(x-L*floor(x/L)): # tao cac chu ky khac
> sp := plot(J1(x), x = -3*L .. 3*L, color = blue, thickness = 3): sp;
Ta bắt đầu tính hệ số Fourier bằng việc khai báo
>assume(m, posint): # khai bao m la so nguyen
Ta bắt đầu tính hệ số Fourier của $J(x)$ như sau:
> a0 := (Int(J(x), x = 0 .. L))/L; a0 := value(a0); # tinh he so Fourier hang
/2 Pi
| Pi - x
| ------ dx
| 2 Pi
/0
-----------------
2 Pi
0
> a[m] := 2*(Int(J(x)*cos(2*m*Pi*x/L), x = 0 .. L))/L;# tinh he so Fourier cosine
/2 Pi
| (Pi - x) cos(m x)
| ----------------- dx
| 2 Pi
/0
----------------------------
Pi
> b[m] := 2*(Int(J(x)*sin(2*m*Pi*x/L), x = 0 .. L))/L; # tinh he so Fourier sine
/2 Pi
| (Pi - x) sin(m x)
| ----------------- dx
| 2 Pi
/0
----------------------------
Pi
> a[m] := value(a[m]); b[m] := value(b[m]);
0
1
----
Pi m
> a := unapply(a[m], m); b := unapply(b[m], m);
Ta được chuỗi Fourier của hàm $J(x)$
$$\dfrac{1}{\pi}\sum_{k=1}^\infty \dfrac{\sin(kx)}{k}.$$
Chú ý nhỏ
$$S_n(J, x)=\dfrac{1}{2\pi}\int_0^x \left[D_n(t)-1\right]dt.$$
Đây là điểm dẫn đến việc lý giải hiện tượng Gibb. Để nhìn thấy hiện tượng Gibb của hàm này ta làm như sau:
> with(plots): with(plottools):
> S := proc (n) options operator, arrow; a0+add(a(k)*cos(k*2*Pi*x/L)+b(k)*sin(k*2*Pi*x/L), k = 1 .. n) end proc; # lap tong Dirichlet
> maxn := 10:
> for n from 0 to maxn do pl[n] := display([sp, plot(S(n), x = -3*L .. 3*L, color = [red], title = cat("n = ", convert(n, string)))]) end do;
> display([seq(pl[n], n = 0 .. maxn)], insequence = true);
Cụ thể ta được hình ảnh
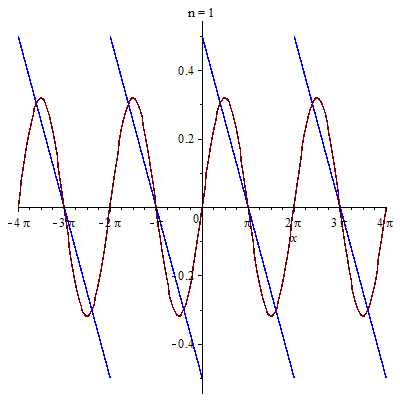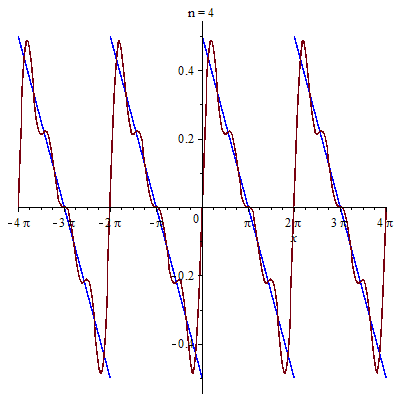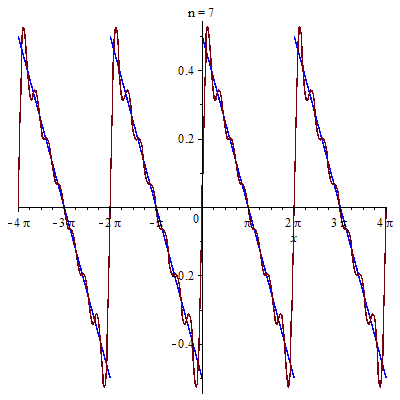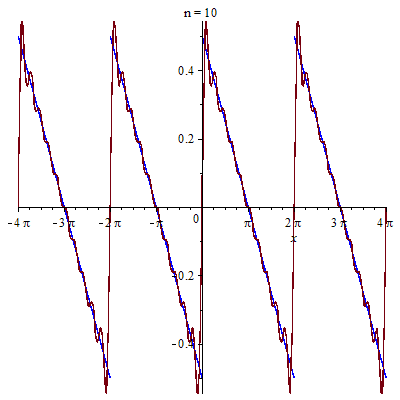
Các bạn thử khai triển Fourier của hàm tuần hoàn chu kỳ $2\pi$ sau
$$f(x)=\begin{cases}\sqrt{x}\sin\left(\dfrac{\pi^2}{x}\right) \; khi \; 0<x\le\pi,\\ 0\; khi \; \pi<x\le 2\pi.\end{cases}$$
Đồ thị hàm này



