Trên một đường tròn cho trước, ta đánh dấu một điểm cố định. Ta sẽ quan sát chuyển động của điểm đánh dấu này khi đường tròn đã cho lăn trên đường thẳng và lăn trên đường tròn.
Khi đường tròn đã cho lăn trên đường thẳng ta có hình ảnh
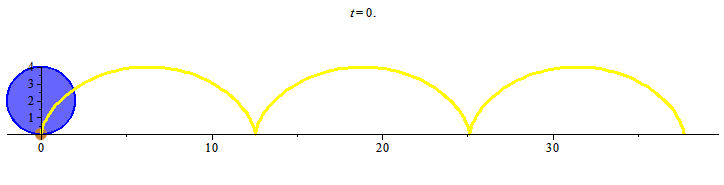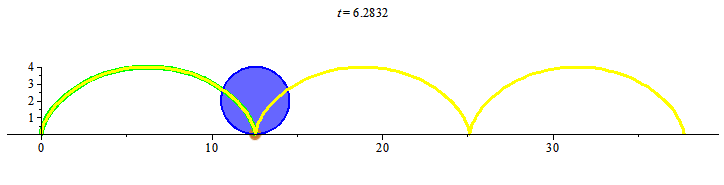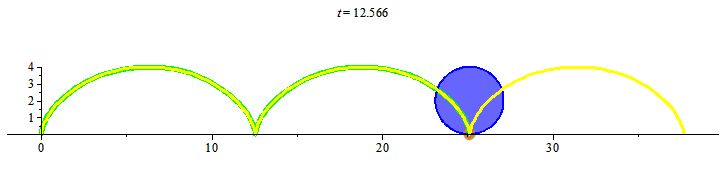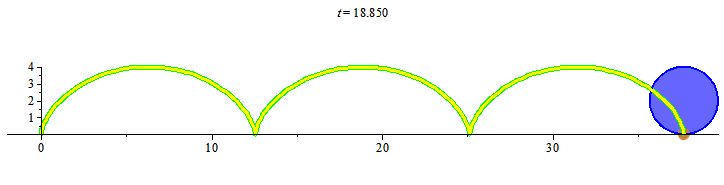
Khi đó điểm đánh dấu chuyển động trên đường cong mà ta gọi là đường cycloid. Đường cong cycloid như trong hình vẽ, đường màu vàng, có phương trình tham số như sau
$$x=2(t-\sin(t)), \; y=2(1-\cos(t)), t\ge 0.$$
Vẽ hình động trên bởi Maple không khó như sau:
> restart; with(plots); with(plottools);
> G := proc (t) plots[display](pointplot([[2*t-2*sin(t), 2-2*cos(t)]], color = gold, symbol = solidcircle, symbolsize = 20), plottools[line]([2*t-2*sin(t), 2-2*cos(t)], [2*t, 2], color = red, thickness = 3), plot([2*u-2*sin(u), 2-2*cos(u), u = 0 .. t], color = green, thickness = 5), plot([2*t+2*sin(u+t), 2+2*cos(u+t), u = 0 .. 6*Pi], filled = true, color = blue)) end proc;
> animate(G, [t], t = 0 .. 6*Pi, background = plot([2*(u-sin(u)), 2*(1-cos(u)), u = 0 .. 6*Pi], color = yellow, thickness = 3), scaling = constrained);
Đường cycloid có nguồn gốc khá tự nhiên. Liệu nó còn có cái gì khác nữa không?
Câu trả lời thứ 1: nó là đường đoản thời ( brachistochrone) theo nghĩa như sau.
Lấy hai điểm $A, B$ trong không gian sao cho $A$ cao hơn $B$, so với mặt đất. Với cái nhìn thông thường thì đoạn thẳng nối $A$ và $B$ là đường có độ dài ngắn nhất trong tất cả các đường nối $A$ và $B.$ Tiếp đến ta quan sát một chất điểm rơi tự do, nghĩa là nó chỉ chịu tác động của trọng lượng. Câu hỏi: trong tất cả các đường nối $A$ và $B$, đường nào là đường đoản thời nghĩa là đường mà chất điểm rơi tự do từ $A$ theo đường đó đến $B$ với thời gian nhanh nhất? Câu trả lời: không phải đoạn thẳng nối $A$ và $B$, mà là đường cycloid nối hai điểm này. Ta nhìn thấy điều này qua hình ảnh sau:
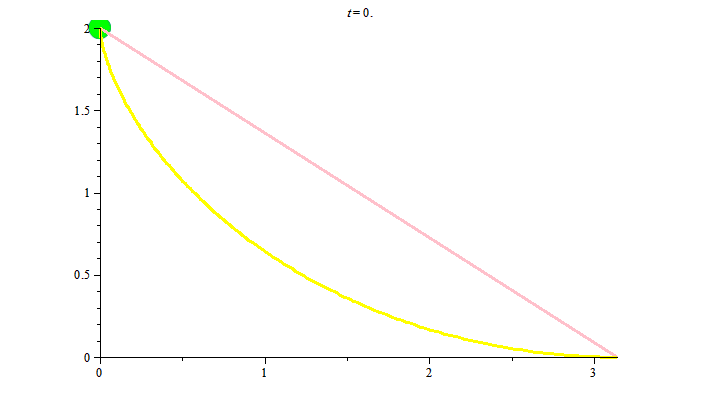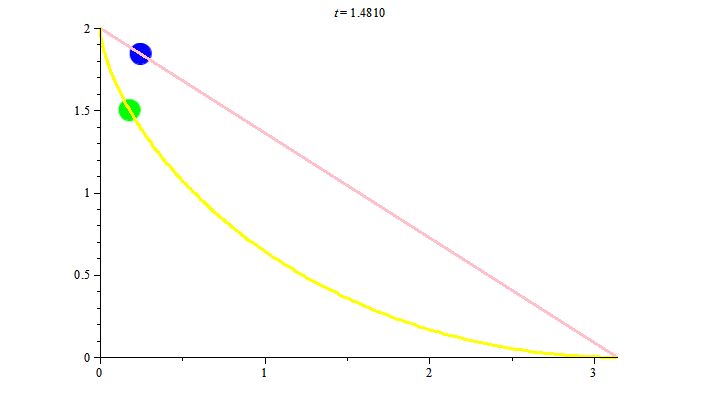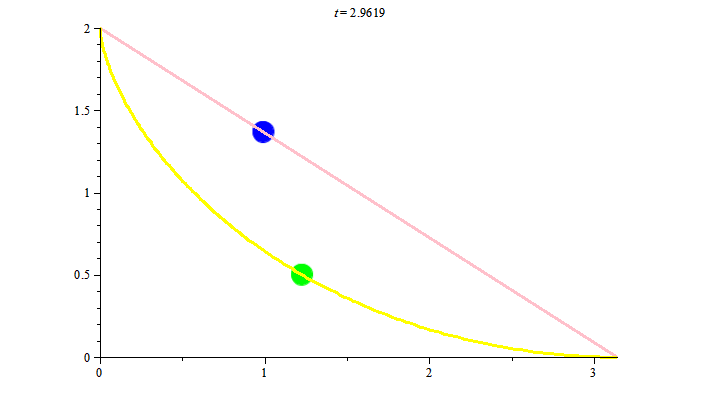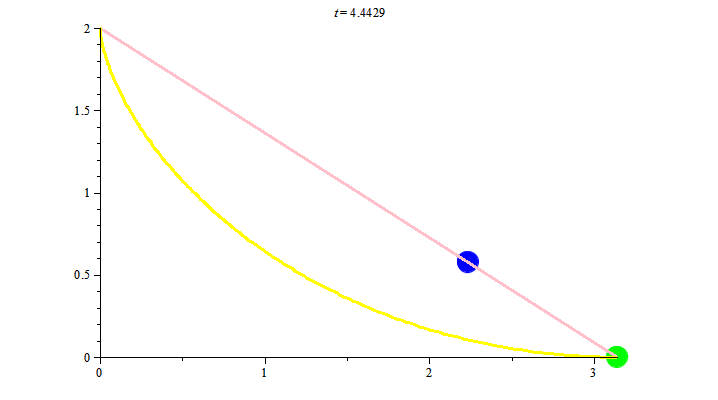
Để vẽ hình trên, đặc biệt chuyển động của các chất điểm ta cần đưa ra tham số hóa hợp lý cho các đường như sau:
+ Đoạn thẳng nối hai điểm:
$$x(s)=x_A+a(s)(x_B-x_A), y(s)=y_A+a(s)(y_B-y_A), s\in [0, T_1]$$
sao cho $a(0)=0, a(T_1)=1$ và tốc độ của chuyển động
$$\sqrt{[x'(s)]^2+[y'(s)]^2}=C\sqrt{y_A-y(s)}$$
trong đó $C$ là hằng số phụ thuộc và gia tốc trọng trường và khối lượng của chất điểm.
+ Đường cycloid nối hai điểm
$$x(s)=R(f(s)-\sin(f(s))), y(s)=R(1+\cos(f(s))), s\in[0, T_2]$$
sao cho $x(0)=x_A, x(T_2)=x_B, y(0)=y_A, y(T_2)=y_B$ và tốc độ của chuyển động
$$R|f'(s)|\sqrt{2-2\cos(f(s))}=C\sqrt{y_A-y(s)},$$
trong đó hằng số $C$ giống như trên. Để đơn giản ta giả sử $C=1.$
Với trường hợp đoạn thẳng nối hai điểm không khó để ta giải phương trình vi phân để tìm $a(s).$ Với trường hợp đường cycloid nói chung khó giải được nghiệm chính xác. Tuy nhiên với hai điểm
$$A=(0, 2), \; B=(\pi, 0)$$
ta tham số hóa chuyển động của chất điểm trên đường cycloid như sau
$$x(s)=\dfrac{s}{\sqrt{2}}-sin\left(\dfrac{s}{\sqrt{2}}\right), \; y(s)=1+\cos\left(\dfrac{s}{\sqrt{2}}\right), s\in[0, \pi\sqrt{2}],$$
và tham số hóa chuyển động của chất điểm trên đoạn thẳng:
$$x(s)=\dfrac{\pi s^2}{2(\pi^2+4)}, \; y(s)=2-\dfrac{s^2}{\pi^2+4}, s\in[0, \sqrt{2(\pi^2+4)}],$$
Đến đây ta dễ dàng đưa ra cách vẽ bằng Maple như sau:
> g1 := proc (t) options operator, arrow; t-sin(t) end proc; f1 := proc (t) options operator, arrow; 1+cos(t) end proc; g2 := proc (t) options operator, arrow; (1/2)*t*Pi end proc; f2 := proc (t) options operator, arrow; 2-t end proc;
> bi := plot([[g1(t), f1(t), t = 0 .. Pi]], thickness = 3, color = yellow, linestyle = [dash, solid]); th := plot([g2(t), f2(t), t = 0 .. 2], thickness = 3, color = "Pink");
> TH := proc (t) plots[display](pointplot([[g2(t^2/(Pi^2+4)), f2(t^2/(Pi^2+4))]], color = blue, symbol = solidcircle, symbolsize = 30), pointplot([[g1(t/sqrt(2)), f1(t/sqrt(2))]], color = green, symbol = solidcircle, symbolsize = 30)) end proc:
> animate(TH, [t], t = 0 .. sqrt(2)*Pi, background = display(th, bi), scaling = constrained);
Chứng minh như trên bằng hình vẽ về tính đoản thời của đường cycloid có lẽ không thuyết phục hoàn toàn. Người đầu tiên đưa ra chứng minh thuyết phục có lẽ là Johann Bernoulli. Cách chứng minh sử dụng nguyên lý khúc xạ ánh sáng của Fermat. Một cách tiếp cận khác sử dụng phương pháp biến phân. Tôi không bàn tiếp về các chứng minh này. Thay vào đó có một câu hỏi nhỏ:
Liệu với hai điểm $A, B$ bất kỳ, ta luôn có thể xây dựng được một đường cycloid đi qua chúng? Nếu xây dựng được thì có thể xây dựng được mấy đường?
Trước khi tiếp tục, ta thấy được điều thú vị: "Đường thẳng chưa chắc cho ta lời giải tối ưu. Đường thẳng đôi khi không phải đường đi nhanh nhất."
Đường cycloid có tính đoản thời. Nó còn có tính đẳng thời (tautochrone) theo nghĩa sau:
Các chất điểm chuyển động trên đường cycloid chỉ dưới tác động của trọng lực. Khi đó thời gian từ lúc chất điểm ở vị trí cao nhất đến vị trí thấp nhất là như nhau. Ta lại xem hình ảnh
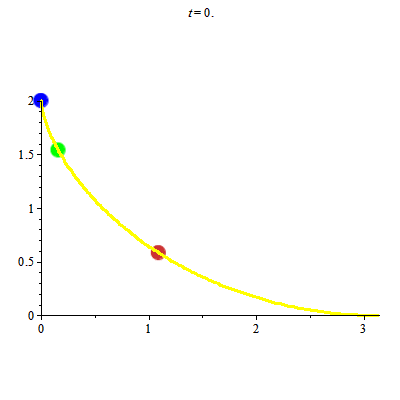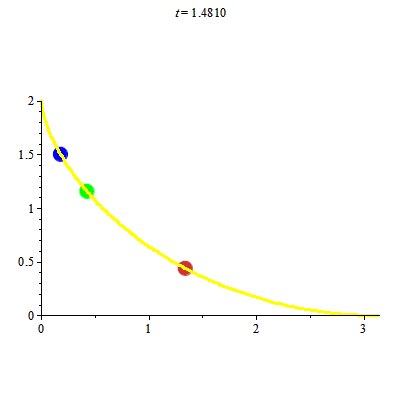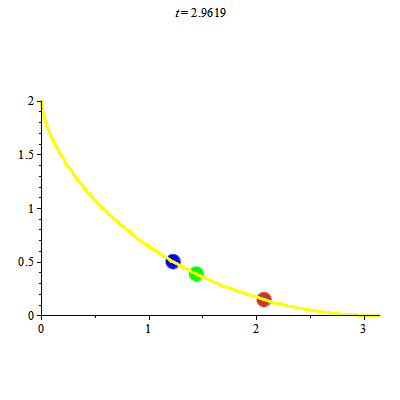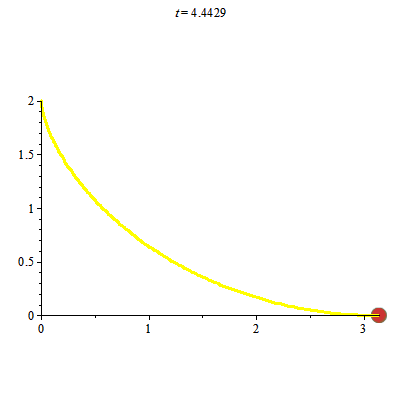
Để vẽ hình ảnh trên ta thực sự phải đối mặt với việc giải bài toán Cauchy
$$f'(s)\sqrt{2-2\cos(f(s))}=\sqrt{\cos(f_0)-\cos(f(s))}, s>0, $$
$$ f(0)=f_0\in (0, 2). $$
Khi $f_0=0$ ta có lời giải đẹp như trên. Tôi không biết cách giải phương trình phi tuyến trên trong trường hợp tổng quát. Tôi tìm trên mạng có vài lời giải gần đúng.
Lời giải tuyến tính khá đơn giản
$$f(s)=f_0+s\left(1-\dfrac{f_0}{\pi\sqrt{2}}\right), s\in[0, \pi\sqrt{2}].$$
Tuy nhiên nó mắc ngay lỗi:
$f'(0)\not=0$ hay nói cách khác vận tốc ban đầu, tại vị trí cao nhất, khác $0.$
Lời giải thứ hai phức tạp hơn
$$f(s)=2\arccos\left(\cos\left(\dfrac{s}{2\sqrt{2}}\right)\cos\left(\dfrac{f_0}{2}\right)\right), s\in[0, \pi\sqrt{2}].$$
Các bạn thử dùng lời giải này để vẽ xem sao?
Như vậy việc chứng minh nhờ hình vẽ không thực sự thuyết phục. Tuy nhiên nó cho ta trực giác nhất định. Chứng minh tính đẳng thời của đường cycloid lại dựa vào tích phân phụ thuộc tham số
$$I(\theta_0)=\int_{\theta_0}^{\pi}\sqrt{\dfrac{1-\cos\theta}{\cos\theta_0-\cos\theta}}d\theta, \theta_0\in(0, \pi).$$
Các bạn thử chứng minh tích phân $I(\theta_0)$ là hàm hằng?
Một ứng dụng thú vị của đường cycloid: con lắc Huygens (Huygens pendulum). Hình ảnh dao động các con lắc Huygens
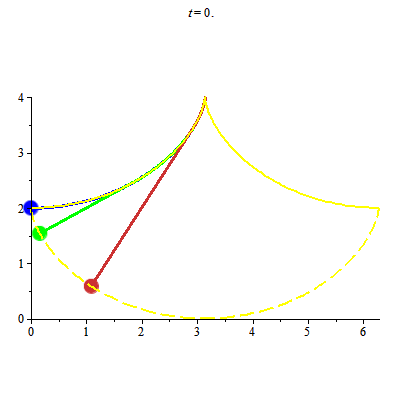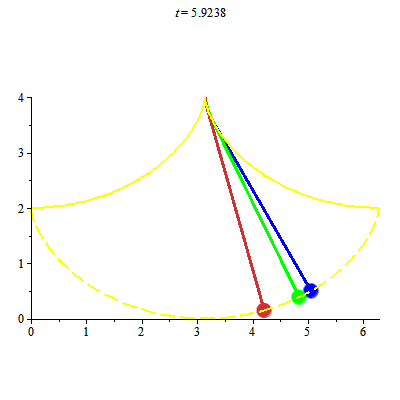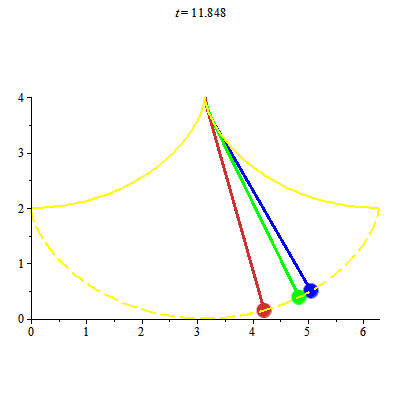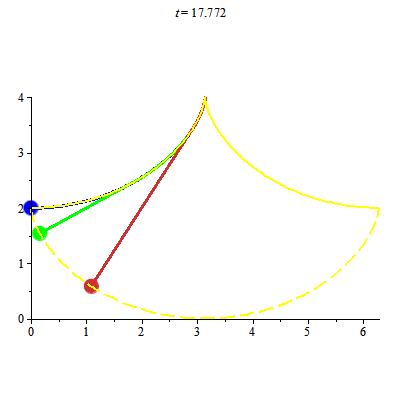
Con lắc Huygens khắc phục được nhược điểm của con lắc thông thường như sau:
+ Với con lắc thông thường, chu kỳ dao động sẽ phụ thuộc vào biên độ dao động khi biên độ dao động không nhỏ.
+ Christiaan Huygens đưa thêm đường cycloid vào, nhờ đó chu kỳ dao động không còn phụ thuộc vào biên độ dao động. Để chứng minh điều này một cách chặt chẽ ta lại cần đến tích phân phụ thuộc tham số
$$J(\theta_0)=\int_0^{\theta_0}\sqrt{\dfrac{1+\cos\theta}{\cos\theta-\cos\theta_0}}d\theta, \theta_0\in(0, \pi).$$
Điều thú vị nữa, quả lắc Huygens chuyển động trên đường cycloid. Cụ thể, nếu con lắc có chiều dài được treo tại $(\pi, 4)$ và dao động trong đường cycloid (liền, màu vàng), Huygens thêm vào
$$x=t+\sin(t), \; y=3-\cos(t), t\in[0, 2\pi],$$
thì quả lắc chạy trên đường cycloid (đứt nét, màu vàng)
$$x=t-\sin(t), \; y=1+\cos(t), t\in[0, 2\pi].$$
Hơn nữa, đường thẳng qua hai điểm
$$(t+\sin(t), 3-\cos(t)), \; (t-\sin(t), 1+\cos(t)), t\in[0, 2\pi]$$
tiếp xúc với đường cycloid Huygens thêm vào. Nhận xét này giúp cho việc vẽ hình trên trở nên dễ dàng như sau:
> g1 := proc (t) options operator, arrow; t-sin(t) end proc; f1 := proc (t) options operator, arrow; 1+cos(t) end proc; h0 := proc (t) options operator, arrow; 2*arccos(cos((1/2)*t/sqrt(2))*cos(0)) end proc; h1 := proc (t) options operator, arrow; 2*arccos(cos((1/2)*t/sqrt(2))*cos(1/2)) end proc; h2 := proc (t) options operator, arrow; 2*arccos(cos((1/2)*t/sqrt(2))*cos(1)) end proc; g3 := proc (t) options operator, arrow; t+sin(t) end proc; f3 := proc (t) options operator, arrow; 3-cos(t) end proc;
> bi := plot([[g1(t), f1(t), t = 0 .. 2*Pi], [g3(t), f3(t), t = 0 .. 2*Pi]], thickness = 2, color = yellow, linestyle = [dash, solid]);
> B := proc (t) plots[display](pointplot([[g1(h0(t)), f1(h0(t))]], color = blue, symbol = solidcircle, symbolsize = 30), plottools[line]([g1(h0(t)), f1(h0(t))], [g3(h0(t)), f3(h0(t))], color = blue, thickness = 3), plot([g3(u), f3(u), u = h0(t) .. Pi], color = blue, thickness = 3), pointplot([[g1(h1(t)), f1(h1(t))]], color = green, symbol = solidcircle, symbolsize = 30), plottools[line]([g1(h1(t)), f1(h1(t))], [g3(h1(t)), f3(h1(t))], color = green, thickness = 3), plot([g3(u), f3(u), u = h1(t) .. Pi], color = green, thickness = 3), pointplot([[g1(h2(t)), f1(h2(t))]], color = orange, symbol = solidcircle, symbolsize = 30), plottools[line]([g1(h2(t)), f1(h2(t))], [g3(h2(t)), f3(h2(t))], color = orange, thickness = 3), plot([g3(u), f3(u), u = h2(t) .. Pi], color = orange, thickness = 3)) end proc;
> animate(B, [t], t = 0 .. 4*sqrt(2)*Pi, background = display(bi), scaling = constrained);
Đường cycloid xuất hiện khi đường tròn lăn trên đường thẳng. Đường tròn lăn quanh đường tròn khác cùng bán kính cho ta đường cardioid.
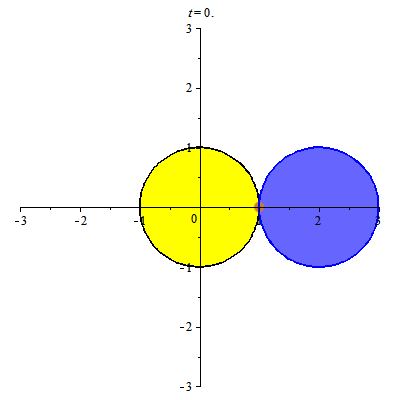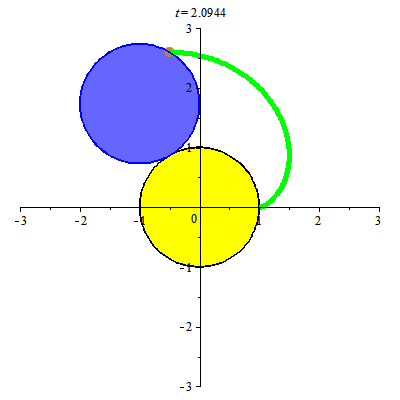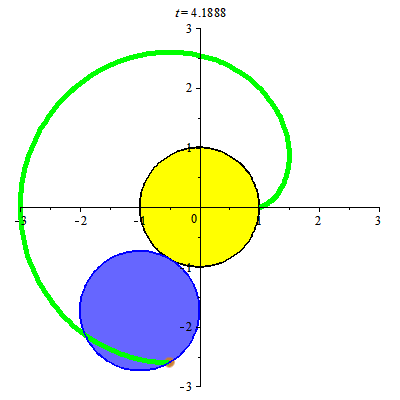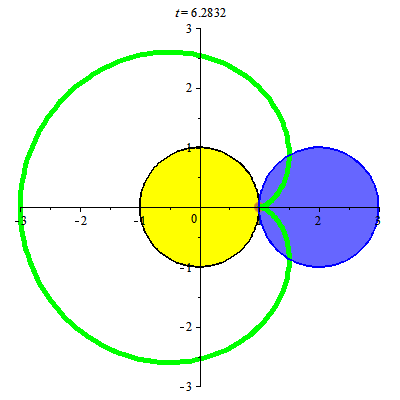
Đường cardioid xuất hiện trong hiện tượng quang học

Nó còn xuất hiện trong hàm biến phức một biến theo cách sau:
Xét ánh xạ bảo giác
$$z\mapsto z^2.$$
Ánh xạ bảo giác này biến các đường tròn đi qua gốc thành đường cardioid. Chẳng hạn đường tròn $|z-1/2|=1/2$ biến thành
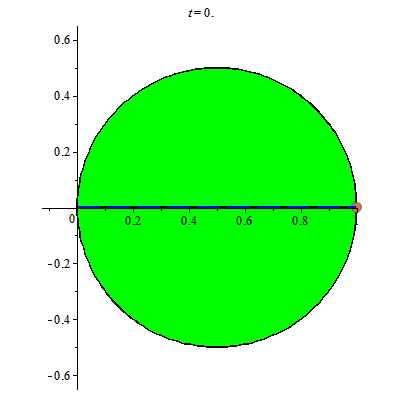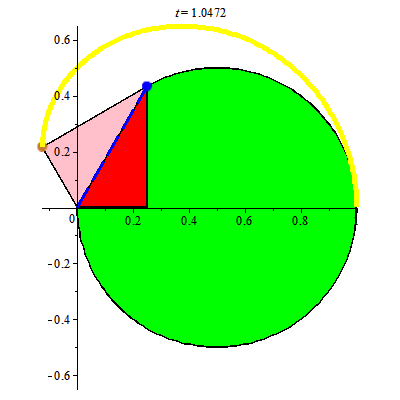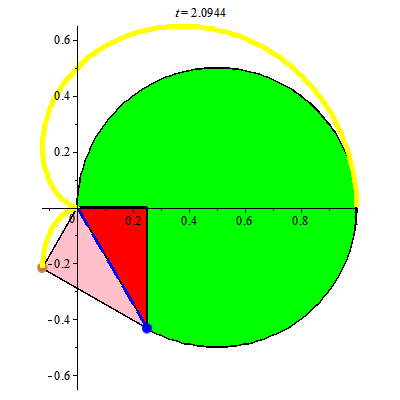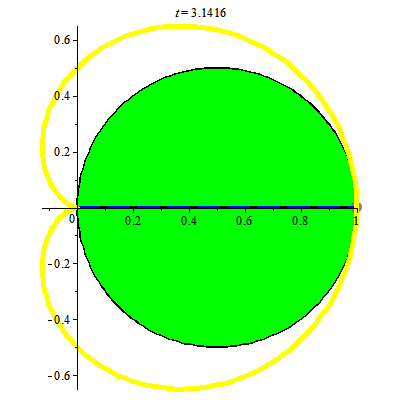
Vẽ các hình trên bằng Maple như sau:
> restart; with(plots); with(plottools);
> dis := display(disk([0, 0], 1, color = yellow)); car := plot([2*cos(u)-cos(2*u), 2*sin(u)-sin(2*u), u = 0 .. 2*Pi], color = yellow, thickness = 3); F := proc (t) plots[display](pointplot([[2*cos(t)-cos(2*t), 2*sin(t)-sin(2*t)]], color = gold, symbol = solidcircle, symbolsize = 20), plot([2*cos(u)-cos(2*u), 2*sin(u)-sin(2*u), u = 0 .. t], color = green, thickness = 5), plot([2*cos(t)-cos(2*u+2*t), 2*sin(t)-sin(2*u+2*t), u = 0 .. 2*Pi], filled = true, color = blue), plottools[line]([2*cos(t)-cos(2*t), 2*sin(t)-sin(2*t)], [2*cos(t), 2*sin(t)], color = red, thickness = 3)) end proc:
> animate(F, [t], t = 0 .. 2*Pi, background = dis, scaling = constrained);
> G := proc (t) plots[display](pointplot([[cos(t)^2, cos(t)*sin(t)]], color = blue, symbol = solidcircle, symbolsize = 20), pointplot([[cos(t)^2*cos(2*t), cos(t)^2*sin(2*t)]], color = gold, symbol = solidcircle, symbolsize = 20), plottools[polygon]([[cos(t)^2, cos(t)*sin(t)], [cos(t)^2, 0], [0, 0]], color = red), plottools[polygon]([[0, 0], [cos(t)^2*cos(2*t), cos(t)^2*sin(2*t)], [cos(t)^2, cos(t)*sin(t)]], color = "Pink"), plottools[line]([0, 0], [cos(t)^2, cos(t)*sin(t)], color = blue, linestyle = dash, thickness = 3), plot([cos(u)^2*cos(2*u), cos(u)^2*sin(2*u), u = 0 .. t], color = yellow, thickness = 5)) end proc:
> animate(G, [t], t = 0 .. Pi, background = display(disk([1/2, 0], 1/2, color = green)), scaling = constrained);
Sửa một chút ánh xạ bảo giác trên thành ánh xạ bảo giác
$$z\mapsto z^2+c$$
là ánh xạ cho ta tập Mandelbrot. Điều thú vị thân trung tâm (central bulb) của tập Mandelbrot chính là cardioid.
Các bạn xem thêm về tập Mandelbrot
https://www.youtube.com/watch?v=BTiZD7p_oTc&list=RDLbWS79Cxykg&index=22
Ta chuyển sang một số chuyển động trong không gian. Chuyển động của Mặt Trăng, Trái Đất quanh Mặt Trời được lý tưởng hóa
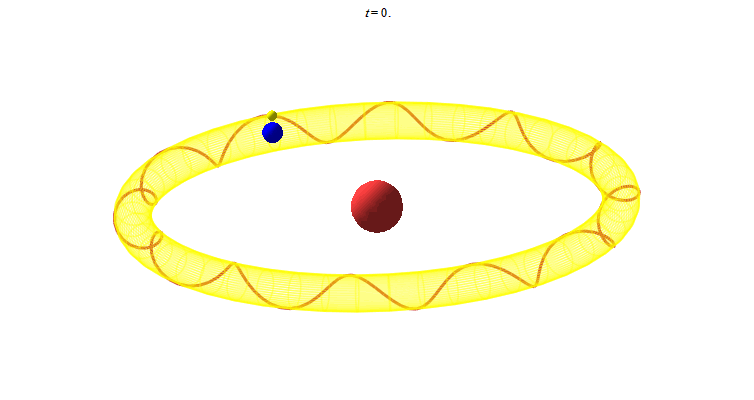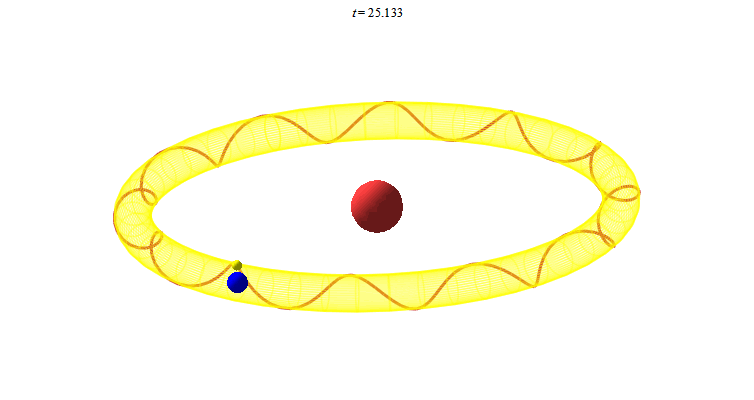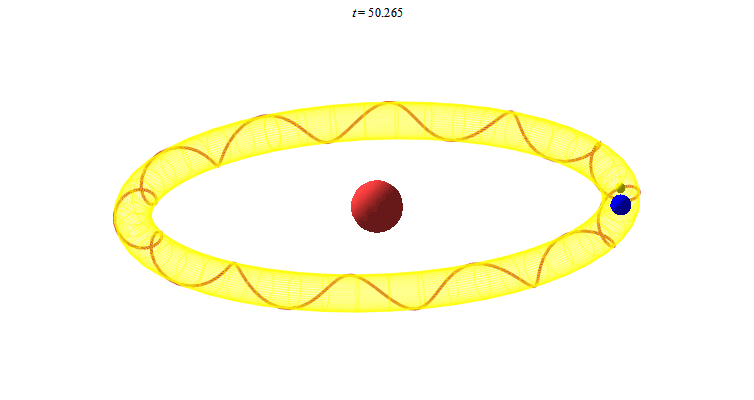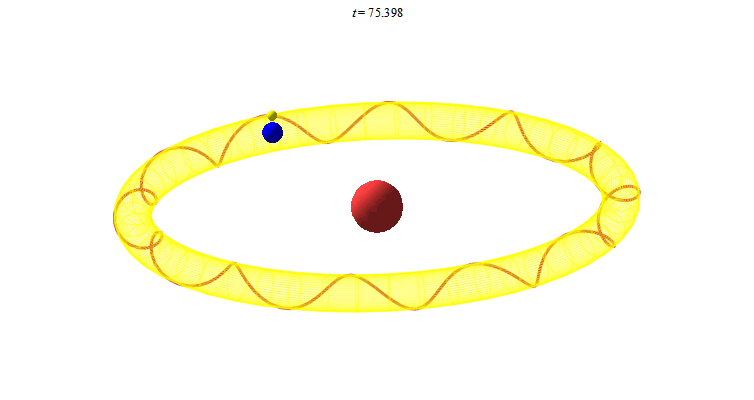
Mặt Trăng chuyển động 12 xoắn trên mặt xuyến chính là 12 tháng trong năm. Vẽ chuyển động này trong Maple như sau:
> restart; with(plots); with(plottools);
> p := proc (t) options operator, arrow; (40+5*sin(t))*cos((1/12)*t) end proc; q := proc (t) options operator, arrow; (40+5*sin(t))*sin((1/12)*t) end proc; r := proc (t) options operator, arrow; 5*cos(t) end proc;
> cyc := spacecurve({[p(12*x), q(12*x), r(12*x), color = orange], [p(12*(x+Pi)), q(12*(x+Pi)), r(12*(x+Pi)), color = orange], [p(12*(x+(1/2)*Pi)), q(12*(x+(1/2)*Pi)), r(12*(x+(1/2)*Pi)), color = orange], [p(12*(x+3*Pi*(1/2))), q(12*(x+3*Pi*(1/2))), r(12*(x+3*Pi*(1/2))), color = orange]}, x = 0 .. (1/2)*Pi, thickness = 3, grid = [100, 100]); cir := spacecurve([40*cos(t), 40*sin(t), 0], t = 0 .. 2*Pi, color = green, thickness = 3, linestyle = dash);
> xuyen := plot3d([(40+5*sin(t))*cos(h), (40+5*sin(t))*sin(h), 5*cos(t)], t = 0 .. 2*Pi, h = 0 .. 2*Pi, color = yellow, style = wireframe);
> G := proc (t) plots[display](pointplot3d([[p(t), q(t), r(t)]], color = yellow, symbol = solidsphere, symbolsize = 15), pointplot3d([[40*cos((1/12)*t), 40*sin((1/12)*t), 0]], color = blue, symbol = solidsphere, symbolsize = 25)) end proc;
> animate(G, [t], t = 0 .. 24*Pi, background = display(cyc, cir, xuyen, pointplot3d([[0, 0, 0]], color = orange, symbol = solidsphere, symbolsize = 50)), scaling = constrained);
Chuyển động thú vị tiếp: chuyển động xoáy từ cực này đến cực kia trên bề mặt Trái Đất:

Để kết thúc bài viết ta thư giãn với vài đường bóng bàn. Nhìn hình ảnh này, người Trung Quốc liên tưởng đến "song ngư", còn người Nhật liên tưởng đến "butterfly".
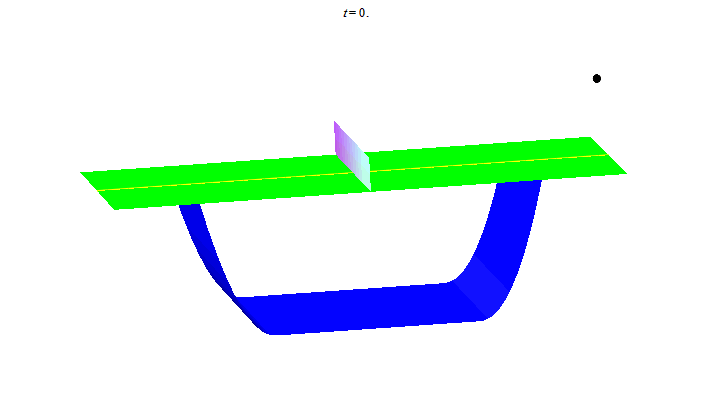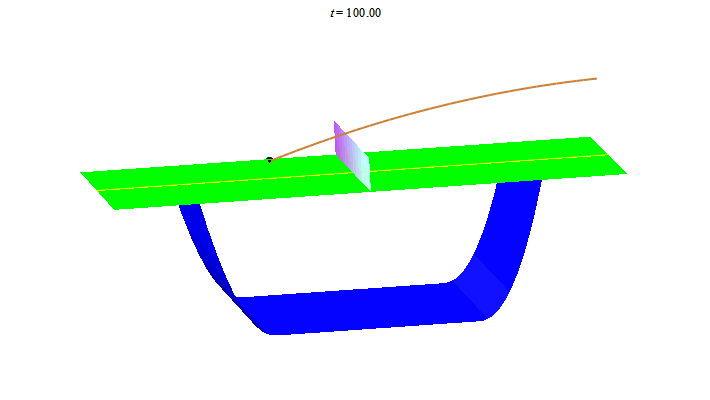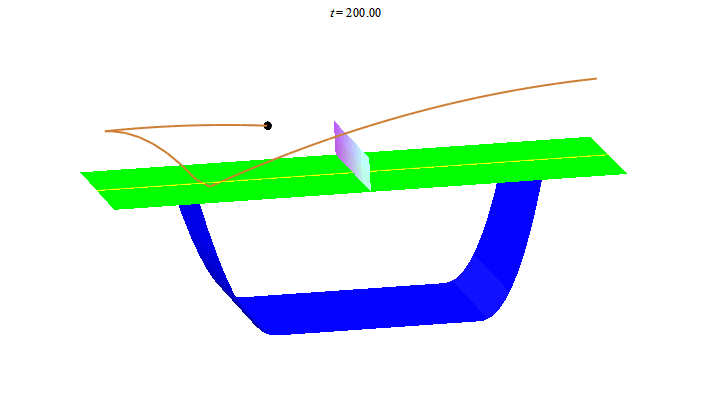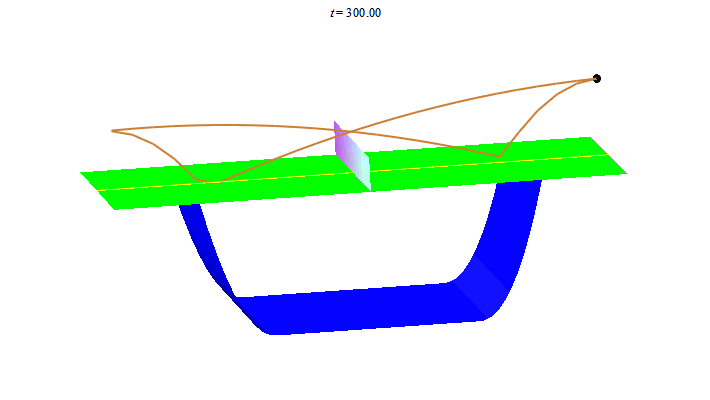
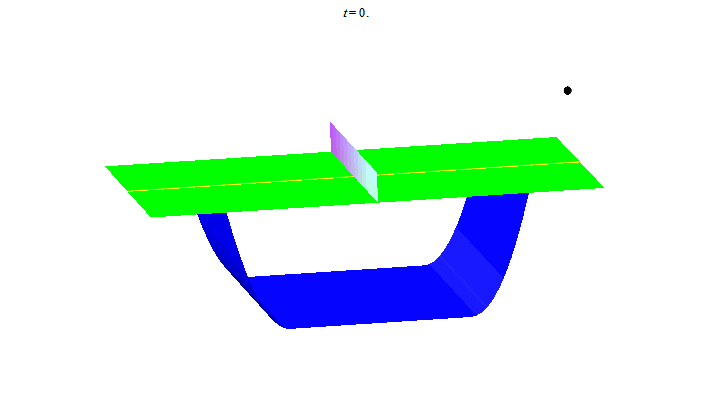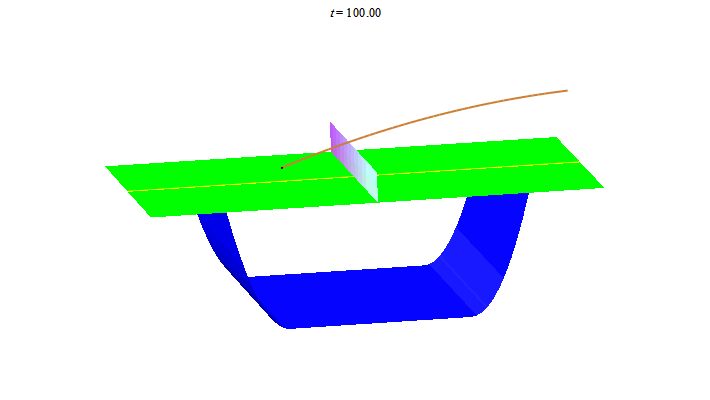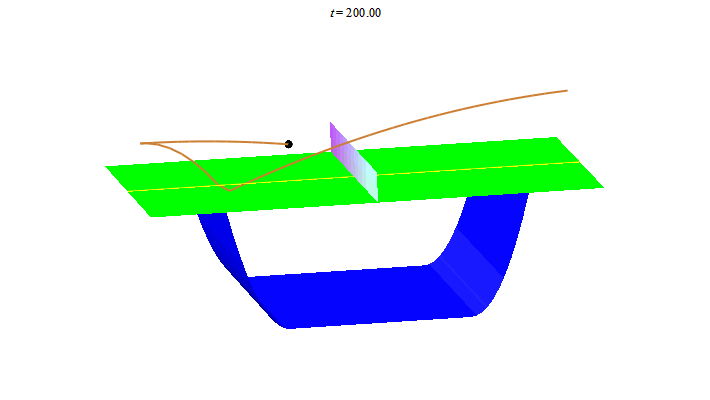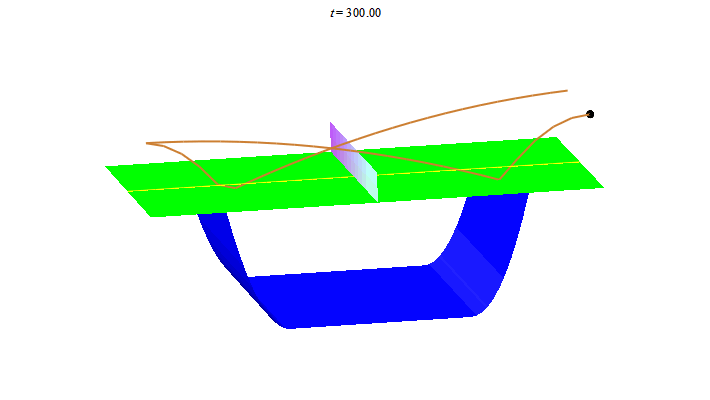
Người Tây lại nghe thấy "ping pong"
https://www.youtube.com/watch?v=yGrbzPOp5Gg


